关于银河的运动
拍摄银河拱桥时,最关键的问题是:银河在天空中从哪里升起、在哪里最高、又往哪里落下?
本篇博客围绕这个核心问题,结合天球几何与向量计算,从原理出发,逐步建立了一套可用于拍摄规划的模型。
0、背景
这次在上都湖拍星,我们把车停在湖边公路上。正好路边有个路牌。我一看还挺适合作地景的,就准备拍个公路银拱。掏出手机软件比划了一下,结果发现道路不在银拱中心,最后只好随便拍了拍了事。
回想一下这次也不是第一次翻车了。上次在库布其沙漠拍英仙座流星雨也是,本来想拍一个竖直银河在地景孤树上方。结果最后发现从我选的机位拍银河,银河根本不会如愿竖直在孤树上方,最后只好选了一张倾斜银河做背景。
痛定思痛,回来后我就研究了一下银河在天球中的运动逻辑,也就有了这篇博客。虽然最初只是想思考一下怎么计算银拱方位与高度的,但研究到最后发现竖直银河一样可以套用,所以这里就一起写了。
1、关于球面投影
在进入数学计算前,首先要理解的一点是:我们在照片中看到的“银拱”,并不代表银河本身真的弯曲成了拱形。这种拱形,其实是由于银河在球形天穹上的位置,通过相机镜头投影到二维图像上所形成的一种球面投影效果。
银河系本身是一个巨大的扁平圆盘结构,地球正好位于这个盘面之中、略偏中心的位置。由于银河盘的厚度有限,大部分恒星、星团和星云都集中分布在这个盘面上。从地球向四周望去,我们就会在天空中看到一条密集的亮带,这就是我们所说的“银河”。
在天球坐标体系中,银河盘在天空中的路径可以抽象为一条大圆,称为“银河赤道”或“银道面”。同样,地平线在天球上也构成另一条大圆。我们之所以能在照片中看到“银拱”,正是因为银河赤道在天空中以一定角度跨越地平线,而这种球面上的几何关系,通过不同的投影方式,会在图像中呈现出完全不同的视觉效果。
比如,在常见的广角投影中,可以让地平线保持为一条平直的线,此时银河则自然形成上拱的弧形,即我们熟悉的“银拱”;如果调整投影轴线,也可以让银河向上拱的同时让地平线向下拱,两者组合起来像一只“眼睛”;而采用“小星球”等极端投影方式时,地平线会围绕画面形成一个圆环,而银河则变成一条穿越“星球”的直线。
2、三种坐标系
想要准确搞清楚银河在天球上的位置和运动,其实说白了就是把一切都量化,用准确的角度和坐标来替代“感觉”。好在这些问题在天文学里早就被研究透了,我们只需要学会怎么用。
除了地理上常用的经纬度坐标(即地图上的“坐标”)外,想要在天球上描述银河,还得了解三种天文学里常用的坐标系统:
- 地平坐标系(Horizontal / Alt-Az):最直观的坐标系,以观测者为中心,描述天体在天空中的位置。参考面是地平面,0°方位角是正北,顺时针旋转到360°。地平坐标系用“方位角”和“高度角”来描述天体在哪个方向、离地多高。
显然,地平坐标系是以观测者为中心、以地平线为参考建立的局部坐标系。它与观测者的地理位置 和观测时间密切相关。因此,哪怕观察的是同一个天体,在不同的时间或地点,其地平坐标都会不同。
- 赤道坐标系(Equatorial / RA-Dec):这是天文学最常用的标准坐标系,参考面是地球赤道在天球上的投影(天球赤道)。0°经度从春分点开始,赤经用小时表示(0h~24h),赤纬则是角度(−90°到+90°)。
赤道坐标系跟恒星背景是固定的,太阳系外的恒星、银河系中心的赤经赤纬是固定不变的。所以查星历表一般都是使用赤道坐标系。
- 银道坐标系(Galactic):从银河系自身角度出发的坐标系,参考面是银道面,原点是太阳,0°经度指向银河系中心(人马座方向)。银河盘面是银纬0°,我们看到的“银拱”基本都在这个平面附近。这个坐标系非常适合描述银河结构。
虽然严格来说,银道坐标系的原点是太阳而不是地球,但在银河系的尺度下,太阳和地球的距离(大约1.5亿公里)几乎可以忽略不计。相比银河直径约10万光年,这点距离根本算不上偏移。因此,在使用上我们可以近似认为原点就是地球,对拍摄银河位置的判断没有任何实质影响。
3、计算银拱方位
在拍摄银拱的时候,我们最关心的其实就是银河在天空中的“走向”。具体来说,有三个关键点最值得关注:
-
银拱的最高点:银河在天空中拱起的最高位置;
-
银河与地平线相交的两个交点:银河从地平线上升起与落下的位置。
为了构图、规划机位与时间,知道这三个点在地平坐标系中的方位角与仰角是非常重要的。
这其实就是一个简单的空间几何问题。为了方便计算与理解,将所有向量统一放在赤道坐标系中处理。
计算涉及两个面:银道面与地平面。这两者分别用其法向量表示。地平面的法向量就是某个时间与地点下,观测者“天顶方向”的赤道坐标系坐标。而银道面法向量在赤道坐标系中是固定的,赤经(RA)约为 192.85948°、赤纬(Dec)约为 27.12825°
从天球几何上看,这两个面的交线决定了银河与地平面的交点,而银拱的最高点则是地平面法线在银道面中的投影方向。
具体运算中,我们将银道面与地平面的法向量都表示为单位向量,统一在赤道坐标系中定义。设银道面的法向量为 \(n_{\text{gal}}\),地平面的法向量为 \(n_{\text{horizon}}\)。这两个面的交线方向可以通过向量叉乘得到:
\(v_{\text{intersection}}\) 及其反方向分别指向银河与地平线的两个交点,将这正反两个单位向量转换为地平坐标,即可获得银河升起与落下的方向。其中由于它们都落在地平面上,因此仰角为 0°。
而银拱的最高点是在银道面中,与交线垂直、朝向天顶的方向。所以可以通过另一个叉乘得到:
得到\(v_{arch\_top}\)后,同样可以将其转换为地平坐标,得到银拱最高点仰角与方位角。
具体的代码见附录。
4、关于银河的运动
为了更直观地理解银河在天空中的运动,我们进一步研究银河是如何在天球中随时间变化的。
由于银河与地平线的两个交点可以从银拱最高点的方位角 ± 90° 推出,我们可以将问题简化为:只关注银拱最高点在地平坐标系中的运动轨迹。掌握了它的方位角与仰角的变化,也就等于掌握了整条银河在天空中的“走向”如何演变。
我原本尝试推导出一个解析公式,直接表达银拱最高点在给定时间下的地平坐标。但由于地平坐标系会随时间不断变化(因地球自转导致的天球旋转),其变换牵涉坐标旋转,最终导致公式过于复杂,难以简洁表达。
于是我最终采用了更直观可靠的方式:打表计算。通过对一天内多个时刻逐点计算,记录银拱最高点在地平坐标中的方位角与仰角,便可以清楚了解银河在天空中的运动轨迹。
需要说明的是,银河在天球中的位置几乎是恒定不变的。我们所看到的银河随时间移动,其实是由于地球自转引起的天球转动(恒星日约 23 小时 56 分)。这意味着不同日期银河的轨迹,实际上只是时间上的整体平移——每天大约提前 4 分钟。
因此,只要记录一天内银拱最高点的运动轨迹,就可以近似推导出其他日期的结果。这也正是“打表”方法有效的根本原因。
下面的图表展示了北京地区在 6 月 15 日这一天(用了UTC,懒得换算时区了)中,银拱最高点的方位角与仰角随时间的变化曲线。
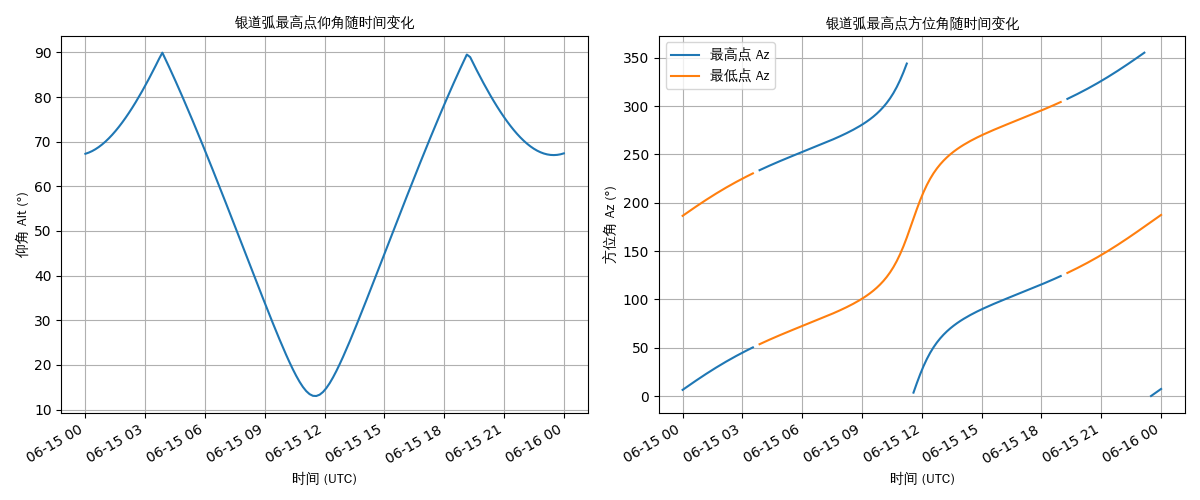
在纬度低于约 63° 的地区,银河会从天顶划过。这时,银拱的最高点会穿过头顶,导致其方位角发生180° 的跳变。为了保持图中轨迹的连贯性,我在“打表”时额外记录了银拱最低点(即仰角为负、处于地平面下方的对称点)的方位角,用于补全曲线,使图像在跳变处连续。同时,对实际跳变段的连线进行了剔除处理,避免错误的视觉连接。
从结果来看,不论观测者位于地球上的哪个纬度,银拱最高点的方位角始终是单调上升的,只是上升的速率随时间和纬度不同而有所变化。虽然这里只展示了北京的结果,但其他纬度的情况也遵循同样的规律。为了精简正文,未在此列出其他纬度的图表,有兴趣的读者可以参考附录中的代码自行生成。
为了帮助理解上面表格中银拱最高点随时间变化的轨迹,我制作了一个简单的 GIF 动画,用以直观展示银河在天球中的运动。动画中:
-
中央的深蓝色球体代表天球;
-
紫色的轴线表示地轴(指向天球的南北极);
-
水平的圆盘表示地平面,模拟的是北京地区(纬度约 40°)的观察视角;
-
随时间旋转的圆环表示银河在天球上的位置变化;
-
圆环上红蓝交界处的为银心方向。
这个动画展示了银河如何在地平面上缓慢旋转,从而带来银拱最高点方位角与仰角的变化。

附录
基本都是用llm生成+手动调整的代码,主打一个能跑就行。
milky_way_direction.py
输入时间地点,输出银拱最高点和银河与地平线相交的两个交点。
import numpy as np
from astropy.time import Time
from astropy.coordinates import EarthLocation, AltAz, ICRS, SkyCoord, CartesianRepresentation
import astropy.units as u
# ====== 1. 基本设置 ======
obs_lat = 39.92 # 纬度
obs_lon = 116.38 # 经度
obs_time = Time('2025-06-15T17:00:00') # UTC
location = EarthLocation(lat=obs_lat*u.deg, lon=obs_lon*u.deg)
altaz_frame = AltAz(obstime=obs_time, location=location)
# ====== 2. 求银道面法线与地平面法线 ======
# 所有运算在赤道坐标系(ICRS)下进行
north_galactic_pole = SkyCoord(l=0*u.deg, b=90*u.deg, frame='galactic')
north_gal_icrs = north_galactic_pole.transform_to(ICRS())
n_gal = np.array(north_gal_icrs.cartesian.xyz.value)
print(f"银道面法线(赤道坐标系):")
print(f" 赤经 RA = {north_gal_icrs.ra.deg:.2f}°")
print(f" 赤纬 Dec = {north_gal_icrs.dec.deg:.2f}°")
zenith = SkyCoord(alt=90*u.deg, az=0*u.deg, frame=altaz_frame)
zenith_icrs = zenith.transform_to(ICRS())
n_h = np.array(zenith_icrs.cartesian.xyz.value)
print(f"地平面法线(赤道坐标系):")
print(f" 赤经 RA = {zenith_icrs.ra.deg:.2f}°")
print(f" 赤纬 Dec = {zenith_icrs.dec.deg:.2f}°")
# ====== 3. 求银道面与地平面的交线方向 ======
# 这是银道面和地平面的交线方向(沿银道弧在地平线上升下落方向)
# 两平面法向量的叉积就是交线方向
vec_galactic_horizon_cross = np.cross(n_gal, n_h)
vec_galactic_horizon_cross /= np.linalg.norm(vec_galactic_horizon_cross)
# ====== 4. 求银拱在地平坐标中最高点方向 ======
# 这是银拱在地平坐标中最高点所指的方向
# 这个方向位于银道面内,并垂直于上面那条交线
vec_galactic_arch_top = np.cross(vec_galactic_horizon_cross, n_gal)
vec_galactic_arch_top /= np.linalg.norm(vec_galactic_arch_top)
# ====== 5.转换回地平坐标系并输出 ======
sc_cross = SkyCoord(CartesianRepresentation(*vec_galactic_horizon_cross),
frame=ICRS())
h_cross = sc_cross.transform_to(altaz_frame)
az_cross = h_cross.az.deg % 360
alt_cross = h_cross.alt.deg
print(f"银道与地平交线方向(升落点):")
print(f" 方位角 Az = {az_cross:.2f}°")
print(f" 方位角 Az = {(az_cross+180)%360:.2f}°")
sc_top = SkyCoord(CartesianRepresentation(*vec_galactic_arch_top),
frame=ICRS())
h_top = sc_top.transform_to(altaz_frame)
az_top = h_top.az.deg % 360
alt_top = h_top.alt.deg
print(f"银道弧最高点方向:")
print(f" 方位角 Az = {az_top:.2f}°")
print(f" 仰角 Alt = {alt_top:.2f}°")
arch_top_movement.py
输入坐标与时间,计算一天内银拱的最高点的运动图表。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from astropy.time import Time
from astropy.coordinates import EarthLocation, AltAz, ICRS, SkyCoord, CartesianRepresentation
import astropy.units as u
import pandas as pd
# ====== 1. 观测点与时间设置 ======
obs_lat = 40 # 纬度
obs_lon = 116.38 # 经度
location = EarthLocation(lat=obs_lat*u.deg, lon=obs_lon*u.deg)
start_time = Time('2025-06-15T00:00:00') # UTC 时间起点
delta_minutes = 10
num_points = int(24*60 / delta_minutes)
times = start_time + np.linspace(0, 24, num_points) * u.hour
# ====== 2. 银道面法线(固定) ======
north_gal_icrs = SkyCoord(l=0*u.deg, b=90*u.deg, frame='galactic').transform_to(ICRS())
n_gal = np.array(north_gal_icrs.cartesian.xyz.value)
# ====== 3. 逐时间计算最高点方向在地平坐标系下的位置 ======
az_top_list = []
az_bottom_list = []
alt_list = []
for t in times:
altaz_frame = AltAz(obstime=t, location=location)
# 地平法线(天顶方向)
zenith = SkyCoord(alt=90*u.deg, az=0*u.deg, frame=altaz_frame).transform_to(ICRS())
n_h = np.array(zenith.cartesian.xyz.value)
# 银道与地平交线方向
vec_cross = np.cross(n_gal, n_h)
vec_cross /= np.linalg.norm(vec_cross)
# 银道弧最高点方向
vec_top = np.cross(vec_cross, n_gal)
vec_top /= np.linalg.norm(vec_top)
# 转换到地平坐标系
sc_top = SkyCoord(CartesianRepresentation(*vec_top), frame=ICRS()).transform_to(altaz_frame)
az_top_list.append(sc_top.az.deg % 360)
az_bottom_list.append((sc_top.az.deg+180) % 360)
alt_list.append(sc_top.alt.deg)
# 去除az_list跳变(优化折线图显示)
def remove_jumps(az_list):
result = [az_list[0]]
for i in range(1, len(az_list)):
if abs(az_list[i] - az_list[i-1]) > 100: # 如果相邻az差值超过100
result[-1] = None # 将前一个值置为 None
result.append(az_list[i])
return result
az_top_list=remove_jumps(az_top_list)
az_bottom_list=remove_jumps(az_bottom_list)
# ====== 4. 可视化 ======
font_path = "/usr/share/fonts/wenquanyi/wqy-zenhei/wqy-zenhei.ttc"
font_prop = FontProperties(fname=font_path)
time_list = [t.datetime for t in times]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharey=False)
ax1.plot(time_list, alt_list)
ax1.set_title("银道弧最高点仰角随时间变化", fontproperties=font_prop)
ax1.set_xlabel("时间 (UTC)", fontproperties=font_prop)
ax1.set_ylabel("仰角 Alt (°)", fontproperties=font_prop)
ax1.grid(True)
ax2.plot(time_list, az_top_list, label="最高点 Az")
ax2.plot(time_list, az_bottom_list, label="最低点 Az")
ax2.set_title("银道弧最高点方位角随时间变化", fontproperties=font_prop)
ax2.set_xlabel("时间 (UTC)", fontproperties=font_prop)
ax2.set_ylabel("方位角 Az (°)", fontproperties=font_prop)
ax2.grid(True)
ax2.legend(prop=font_prop)
fig.autofmt_xdate()
fig.tight_layout()
plt.show()
plt.savefig("movement.png")
gif生成代码
// 可以通过https://editor.p5js.org/直接生成
let angle = 0;
let observerLat = 40;
function setup() {
createCanvas(600, 600, WEBGL);
angleMode(RADIANS);
frameRate(60);
}
function draw() {
background(255);
lights();
// 摄像机设置
let camRadius = 1000;
let theta = radians(200);
let camX = camRadius * sin(theta);
let camY = camRadius * -cos(theta);
let camZ = 750;
camera(camX, camY, camZ, 0, 0, 0, 0, 0, -1);
// 地平面
noStroke();
fill(180);
box(450, 450, 5);
rotateY(radians(90-observerLat));
rotateZ(radians(angle));
// 球体
noStroke();
fill(50, 50, 100, 255);
sphere(200);
// 赤道坐标极轴(Z轴)
stroke(255, 50, 255); // 极轴
strokeWeight(2);
line(0, 0, -300, 0, 0, 300); // Z轴线
// 渐变银拱
noFill();
strokeWeight(3);
drawGalacticArc(220);
// drawXYZAxes(250);
angle += 2;
// if (frameCount <= 180) {
// saveCanvas('frame_' + nf(frameCount, 4), 'png');
// }
}
function drawXYZAxes(length = 300) {
strokeWeight(2);
// X 轴(红色)
stroke(255, 0, 0);
line(0, 0, 0, length, 0, 0);
// Y 轴(绿色)
stroke(0, 255, 0);
line(0, 0, 0, 0, length, 0);
// Z 轴(蓝色)
stroke(0, 0, 255);
line(0, 0, 0, 0, 0, length);
}
function raDecToVec(ra_h, dec_d) {
let ra = radians(ra_h * 15);
let dec = radians(dec_d);
let x = cos(dec) * cos(ra);
let y = cos(dec) * sin(ra);
let z = sin(dec);
return createVector(x, y, z);
}
function rotateAroundAxis(vec, axis, angle) {
let cosA = cos(angle);
let sinA = sin(angle);
let my_dot = vec.dot(axis);
let my_cross = p5.Vector.cross(axis, vec);
return p5.Vector.add(
p5.Vector.add(
vec.copy().mult(cosA),
my_cross.mult(sinA)
),
axis.copy().mult(my_dot * (1 - cosA))
).normalize();
}
function drawGalacticArc(radius) {
let steps = 200;
// 北银极方向(圆心)
let pole = raDecToVec(192.8595 / 15, 27.1283); // RA:小时, Dec:度
// 银心方向(起点)
let start = raDecToVec(266.4168 / 15, -29.0078);
// 用单位向量绘制
beginShape();
for (let i = 0; i <= steps; i++) {
let t = i / steps;
let angle = t * TWO_PI;
// Rodrigues’ rotation: rotate `start` around `pole`
let v = rotateAroundAxis(start, pole, angle).mult(radius);
// 渐变色:红到蓝
let r = lerp(255, 0, t);
let g = 0;
let b = lerp(0, 255, t);
stroke(r, g, b);
vertex(v.x, v.y, v.z);
}
endShape();
}